高校数学で理解する反応拡散系
※この項では空間パターンは扱いません。ですから反応拡散系ではありませんが、そのままこの名称を使います。
文責:尾崎 淳
いきなり言い切ってしまうが、“反応拡散機構は生物の基本原理”だと筆者は思っている。
それは、このモデルが小難しくってカッコいいから・・ではなく、言われてみれば当然な、ごく当たり前のこと言っているにすぎないのに“生物らしさ”のかなりの部分を説明できるからです。
以前より当ホームページでは簡単な反応拡散系の解説ページを掲載してきました。
実際、何人かの方よりこのページは好評価をいただいたのですが、相変わらず多くの実験生物学者や学生からは難解な概念であると感じているように見受けられました。
しかし「難解なことをやっているからすごい」と受け取られることは我々の本望ではありません。
むしろ数学や専門用語で自説を“難解”に見せている発表・出版物に対しては、「この人は真に理解してはいない」としか私には感じられません。
「真理とは、言われてみれば当たり前のこと」だと思います。 そして反応拡散系も「言われてみれば当たり前のこと」なのです。
反応拡散系の概念はすでに確立してします。 ですから当然この分野の本は容易に手に入ります。
しかし、残念ながら実験生物学者が気安く読めるような本はほとんどありません。 以前書いた解説ページの最後では、この辺の事情を述べておきながら、結局いくつか参考文献を挙げて逃げてしまいました。
今回は、反応拡散機構のエッセンスをどれだけ簡単に理解できるか、にトライしてみました。
使うツールは高校数学の「漸化式」です。
現象をどう表現したいか?が大事
生物らしさ、ってなんでしょうね? 私は、ニョキニョキ伸びたりドクドク拍動するさまに“生物らしさ”を感じます。 だからそれをうまく表現できれば生物学は“一丁あがり”です(あくまでも私個人にとっては、ですよ)。 そういった方向で生物を理解したい人もしくは実験結果を解釈したい人は読み進めてください。 そんな形では生物を理解したくない人には以下は大して役に立ちません(でもその立場を尊重はしますよ。一番大事なのは、どうしたいのか?をハッキリさせることです。そういうことが見えてこない研究・発表が最近多くありません?だから聞いていてつまらん)。
漸化式で反応拡散系を理解する
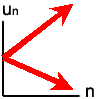
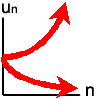
このページでは漸化式で反応拡散系を理解することを目指します。 「漸化式」って高校数学「基礎解析」(今は数学II?A?年がバレるな)で学んだアレです。 基本は等差数列と等比数列です(下図)。 nを時刻と見れば、漸化式は量uの時間変化を表していることになります。 化学(酵素)反応として見れば、公差dや公比rの正・負はそれぞれ合成・分解を意味しています。 一般項が得られれば、それは「未来は完全に予測可能」ということです。 ところが実際の生化学反応ではdやrが複雑なので、まず一般項は得られません。 それでも“dに相当するもの”・“rに相当するもの”は常に似た意味を持っています。 ですから、今後もこの基本数列を意識しながら読み進めてください。
| 漸化式 | 一般項 | 解の振る舞い | |
| 等差数列 | 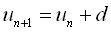 |
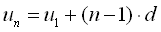 |
 |
| 等比数列 | 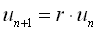 |
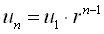 |
 |
現象を漸化式で表現することの利点
漸化式を使う利点は大きく2つあります。
1つ目は、実験生物学者が普段使っている表現に当てはめやすい、ということです。
通常、実験では一つ一つの素過程を解析していきます。 シグナル伝達の上流・下流を明らかにすることは、現象の時間変化を順々に追っていくことです。
つまり頭の中では下図・左3列のような絵が浮かんでいるハズです。
このままでは漸化式にあてはめるには雑過ぎますが、頭の中で起こっていること・・・あぁなって(時刻 n)、次にこうなって(時刻
n+1)、さらにこうなる(時刻 n+2)・・・という言い方はすでに立派な“漸化式流”思考法です。
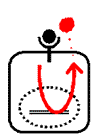
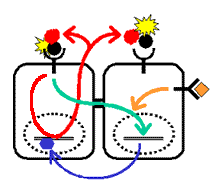
それでは、ここで挙げた例のように現象のつながりが一本線で追っていけるような場合ならば簡単ですが、右図のような場合ではどうでしょうか?
こんなの今までの「あぁなって、こうなって」法では無理ですよね。
そこで漸化式を使う2つ目の利点-シミュレーションへの糸口になる、が挙げられます。 もしかしたら理論家で「いや、私は大体わかるよ」という人がいるかもしれない。しかしそれは、その人がこの分野に慣れ親しんでいて「結果を知っているだけ」にすぎない。予備知識なしに下のネットワークを見て、そのアウトプットをイメージできる人間などチューリングかフォン・ノイマンぐらいだろう。
| 1.あぁなって・・ | 2.そうやって・・ | 3.こうなる、だな | しかし、こうなると、もはや・・ |
 |
 |
 |
 |
近年、実験家で「自分もシミュレーションをやってみたい」という人がチラホラ出始めました。 ところが本屋に行ってみると物理学や工学をやる人が読むような本ばかりで、大学教養でつまらない数学の授業に嫌気が刺して以来、数学とはご無沙汰になっている人には読むのがシンドイものばかりが並んでいます。 理論それ自体の勉強(ほとんどが微分方程式の勉強)とプログラミングの勉強という二重苦のために二の足を踏んでいる人も多いことでしょう。 それを一挙に解決する方法!それは漸化式でやることです。 なぜなら、全てのシミュレーションは漸化式の繰り返し計算(u1を代入してu2を計算→u2を代入してu3を計算→・・・)をしているにすぎないからです。 微分方程式で理解しても最後は漸化式に変換せざるをえないのだから、はじめから漸化式で理論の勉強をしておけば、その知識をすぐにプログラミングに持っていけます。 (もちろん細かいプログラミングの知識不足で初めは計算が発散するでしょうけど、大した問題ではない→プログラミングする際の注意点)
フィードバックで振動は起こる?
上に挙げた等差数列・等比数列は立派な反応式です。 だからこれを素直にプログラミングすれば、ハイ、もう生化学反応のシミュレーションは完成です。 でもこれだけじゃわざわざ“反応拡散系の勉強”というほどでもないですよね。 そもそもシミュレーションするまでもなく結果はイメージできちゃうし。 やっぱり、直感的には「?」と考えてしまうような題材を取り上げないと。 それにはフィードバックが絡む現象、特に振動現象がよいでしょう。
フィードバックはどの教科書にも載っているありふれた概念ですが、いろいろな人と話していて気づいたことがある。
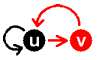
それは、右の図のような負のフィードバックがあれば発現量が振動する、と思っている人が多いことです。
「あぁなって、こうなって」法で言えばこうです。 |
 |
 |
これをシミュレーションしようと考える。 いまの話では、役者は抑制因子だけなので1変数で反応式を書き下せそうだ。 基礎転写として定数dを、濃度依存の抑制効果として-ruを採用して、漸化式:un+1 = un +d -runが書き下せる。 まとめるとun+1 = (1-r)un +d。 つまり(増加の)等差数列と(減少の)等比数列を足しただけです。 大体の振る舞いは上のグラフから想像できますよね? 振動なんてしません!(本当は、rを極端にデカくすると計算上振動しちゃうんだけど・・)一定値に収束しちゃいます。 う〜ん、振動すると思ったのに、なぜだ・・。 結果を知っている理論家からはアッサリと「1変数じゃ振動なんてしないよ」なんて言われて、返す言葉もなくうやむやに・・よくある場面です。 ところがやがて、振動しないフィードバック系でもタイムラグの効果を入れると振動するよ、なんていう論文が出たりする(Lewis, 2003; Monk, 2003)。 これをまた「新しいメカニズムだ!」みたいな感じで提唱されると、どうかなぁ・・と思っている理論家も多いことではないだろうか? だって、そんなことずっと昔から分かっていたことだから。その辺の本屋で売っている“実験家が気安く読めない本”には載ってまっせぇ。
実はこのページを書くきっかけになったのは、この辺のてん末を見ていて、なんだかなぁ・・という気持ちになったからです。実験家も理論家も分かっているような分かっていないような、本質を突いているような突いていないような・・
反応拡散でいいじゃん!全部同じ形で記述できるんだから。
“タイムラグ”だなんて余計な仮定を入れるのは美しくないでしょ。(これ一番大事なこと)
漸化式で記述すれば“タイムラグ”の効果は自然に現れる
これから数式がたくさん出てきます。 でも全て高校数学の範囲です。 厳密さは多少犠牲にしてあります。
でも、そもそも、厳密解(一般項)が解ける場合なんてほとんどないんです(生体反応の厳密解なんて絶対無理!)。
むしろ自分なりのイメージを育んでください。 そのために、なるべく式には図を付けました。
ここで絶対おすすめな見方があります。 以前の解説ページで紹介した、反応速度(a,b,c,d)を自分自身への効果(対角成分:
a, d)と相手からの効果(非対角成分: b, c)とに分ける見方。
これは反応拡散式を直感的に理解する一番わかりやすい見方だと私は思っています。
対角成分は「振幅」、(符号が逆の)非対角成分は「振動」だと言い切っても構いません。 あとはそのバランスで振動したり発散したり収束したりします。
反応拡散系と向き合うときには、まずこの見方で数式を眺めてください。
基本中の基本。
では、何でそれらが振幅および振動を意味しているのだろうか? 次にそれを簡単に説明します。
連立漸化式と3項間漸化式
何やら小難しいタイトルだが、これも全く高校数学の範囲です。
でも当時は、これらに振動の意味があるだなんて教えてくれなかったけど・・
連立漸化式の一般形は、
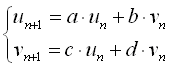
と書けます。これらからvを消去すると3項間漸化式
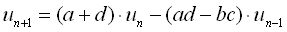
が得られます。いわゆる“ケーリー・ハミルトンの定理”ってやつです(高校でこの名前は出たっけ?)。
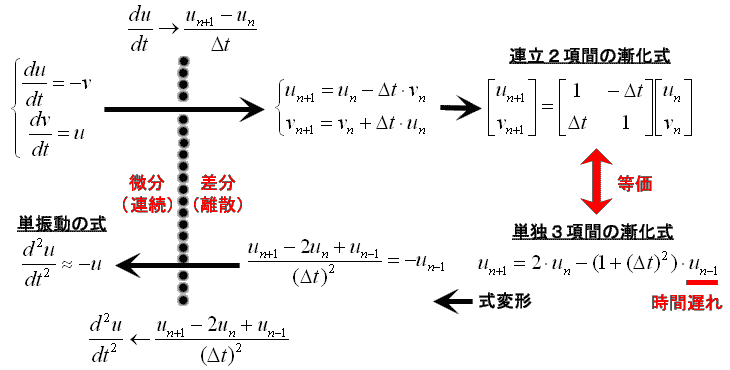
ここで、結果を知っていて書くのも何だが、イメージ優先のため、単振動(振り子やバネの運動)の方程式の式変形を載せちゃいます。
上の列が2変数表記、下の列が1変数表記です。 uを“位置”、vを“速度”と置いて、高校物理を思い出してもらえればイメージが湧きやすいと思います。
ここで改めて上の式の係数がそれぞれ何を意味しているかを確認してください。 逆符号の非対角成分(b,c)が「振動」を表していることがお分かりでしょう。
一方で対角成分(a,d)は「振幅」です。それは(a+d)がunの係数、つまり等比数列の公比に相当していることから明らかです(このページ最初の表参照)。
 |
さてここで注目してもらいたいのは、3項間漸化式のun-1という項の意味です。 もう分かりますよね。 nは時刻を表しているのだから、この項は“タイムラグ”を意味しているのです。 「1変数のフィードバックの式にタイムラグの効果を入れれば振動が生まれる」の正体は、単なる2変数の反応拡散系ということなのです。 厳密には1変数ではないんです。 2変数目を“タイムラグ”という異質の概念に置き換えただけなのです。 ねっ?美しくないでしょ?
これでエッセンスは言い尽くされているのだが、より一般的な形を考えて見よう。連続3項間の漸化式
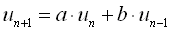
では、un-1 = vnとおくことによって
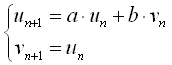 |
 |
 |
 |
という連立2項間の式になる。 その際、新しい変数vは“中間体”という意味を持つ。 では、もっとタイムラグを含んだ次の3項間漸化式ではどうだろうか?
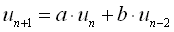
まず上と同じくun-2 = vnとおいてみる。 すると、
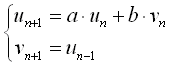
となるが、これではまだ第2式にタイムラグが入ってしまっているので、さらにun-1 = wnとおく。
 |
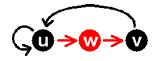 |
 |
 |
これで完成。 「タイムラグが長くなる=中間体の数が多くなる」ということ。あたり前ですよね?
これまでは単純にタイムラグが長くなるにつれて中間体の数を増やしていった。
生物学的に見れば、まぁリーズナブルだが、いくらでも中間体が増えていくとうんざりしますよね?そもそも、そんなに中間体ってあるのか?
これは話を単調にしすぎたためです。全てのタイムラグ(n→n+1)に仮想の中間体をおくのではなく、いくつかの中間体の反応速度を遅くして、その中間体でほとんどのタイムラグを稼いでしまえばよいのです。
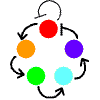
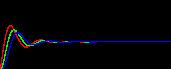
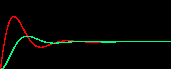
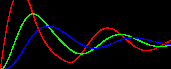
下図は、横には変数の数を増やし、縦には中間体の反応速度Cを変えたときのシステム全体の振る舞いを表したものです(横軸:時間)。
次の特徴を見てください。
・中間体を増やすとタイムラグの効果で振動性が高まっていく。
・2変数であっても、中間体の反応速度を遅くする(=タイムラグ)と振動性が現れる。
| 1変数 | 2変数 | 3変数 | N変数 | |
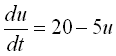 |
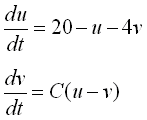 |
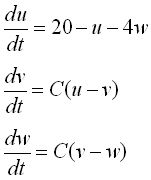 |
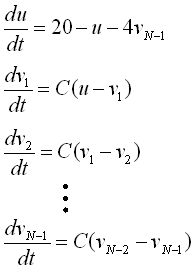 | |
| 反応速度 C |
 |
 |
 |
 |
| 25 (速い) |
 |
 |
 |
 |
| 5 |  |
 |
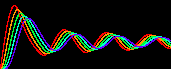 | |
| 1 (遅い) |
 |
 |
 |
上の例では式がシンプルすぎるので振動は最終的には収束しますが(減衰振動)、 下図のように、uの自己触媒を加えると安定した振動状態(リミットサイクル)が生まれます。 面白いことに、基質-消費系では変数の数が奇数のときは振動状態が消え2つの安定状態に分離する。 これは基質-消費系では変数間の振動の位相がほぼ逆になっているためである(2変数のときを見よ)。
| 変数の数 | 活性因子-抑制因子系 |
基質-消費系 |
| 2 | 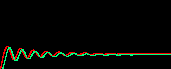 |
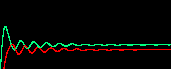 |
| 3 | 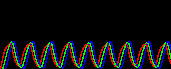 |
 |
| 4 | 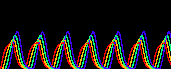 |
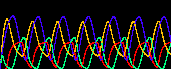 |
| 5 | 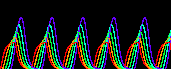 |
 |
| 6 | 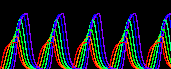 |
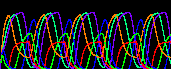 |
以上で本文は終わりです。簡単ですよね?
注意: ここで書いた一連の漸化式は、振動を生み出すエッセンスを説明するために簡略化したものです。 そのままをプログラミングすると、たぶん計算が吹っ飛びます。シミュレーションに興味がある人はこちらも読んでください。→プログラミングする際の注意点
ひとこと物申す
Simple is best!
“すぐれた概念”とは「言われてみれば当然なこと」だし、“すぐれた説明”とは「できるだけ簡潔・明快にそれを理解させられるか」です。 難解な数式や言説を使ったり、分厚い書物に仕上げることは全く逆な行為であることを強調しておきます。
生物系の場で数学専門用語を使うな!
「相空間」とか「特異点」とか「リヤプノフ」とか・・ 数学者同士の会話ならば、そういう単語を使ったほうがむしろ理解が進むだろう。 しかし生物学者を相手に使えば、それは「理解しないでください」と言っているのと同じだ。 自分だって嫌でしょ、会話で相手が知らない単語を連発したら。 私には、そういう発表をする人はプレゼンテーション能力が欠如しているとしか映りません。
応用を意識した数学教育を!
数学の厳密さを軽視しているわけではない。 パズルとしての数学が面白いことも十分に理解している。 でも、ほんの一言見通しの利くコメントを加えてくれるだけで、教わる方としてはだいぶ違うんだけどねぇ。 すべての高校・大学の数学教官は、名著「物理数学の直観的方法」の序文を読んでください(おそらく、ほとんどの物理・工学系の学生はこの本を持っていることだろう)。 ハッキリ言って、この本の登場により、本屋の書棚を埋め尽くす教科書の大部分はいらなくなった、と言ってよいだろう。 今回このページを書くにあたって久しぶりに大学受験の参考書を見た。 漸化式の解き方が書いてあるだけで、その意味するところをコメントしている本は皆無でした。
道具としてのシミュレーション
シミュレーションは“思考の補助手段”として使う道具です。 それ自体が目的にはなりません。 サイエンスは人間の行為ですから、最後は「あぁなって、こうなって」法で理解しないといけないのです。 ただ、脳の限界からか?直観的には考え込んでしまうような現象に当たるときがあります。 そのときに“補助手段”として使うのです。チューリング級の脳ならば大抵のシミュレーションなんて必要ないでしょう。 とりあえず大規模計算してみました・・みたいな発表・論文はナンセンスです!
道具としての反応拡散系
反応拡散系も、今となっては“思考の補助手段”です。 なんで振動するんだろう?なんでパターンができるんだろう?ごちゃごちゃしたシグナル・ネットワークを解きほぐしたいetc.を解決する“補助線”みたいなものです。 パズルに一本補助線を引くだけでグッと見通しがよくなる・・そんな感じですよ。ゲノム・ワイドに解析したって、最後は人間の頭が理解できる形にまとめないといけないんだからね。